Programming Parallel Computers
CP: correlated pairs
Please read the general instructions on this page first, and then check the individual tasks for more details. For each task you can download a zip file that contains the code templates you can use for development.
| Task | Attempts | Points | Max | Rating | Man. | Deadline for full points |
|---|---|---|---|---|---|---|
| CP1: CPU baseline | ||||||
Implement a simple sequential baseline solution. Do not try to use any form of parallelism yet; try to make it work correctly first. Please do all arithmetic with double-precision floating point numbers. For this initial exercise, we have disabled auto-vectorization. |
||||||
| – | – | 5 + 0 | ★ | M | 2024-08-31 at 23:59:59 | |
| CP2a: instruction-level parallelism | ||||||
Parallelize your solution to CP1 by exploiting instruction-level parallelism. Make sure that the performance-critical operations are pipelined efficiently. Do not use any other form of parallelism yet in this exercise. Please do all arithmetic with double-precision floating point numbers. For this technical exercise, we have disabled auto-vectorization. |
||||||
| – | – | 3 + 0 | ★ | M | 2024-08-31 at 23:59:59 | |
| CP2b: multicore parallelism | ||||||
Parallelize your solution to CP1 with the help of OpenMP and multithreading so that you are exploiting multiple CPU cores in parallel. Do not use any other form of parallelism yet in this exercise. Please do all arithmetic with double-precision floating point numbers. For this technical exercise, we have disabled auto-vectorization. |
||||||
| – | – | 3 + 0 | ★ | M | 2024-08-31 at 23:59:59 | |
| CP2c: vectorization | ||||||
Parallelize your solution to CP1 with the help of vector operations so that you can perform multiple useful arithmetic operations with one instruction. Do not use any other form of parallelism yet in this exercise. Please do all arithmetic with double-precision floating point numbers. For this technical exercise, we have disabled auto-vectorization. |
||||||
| – | – | 3 + 0 | ★ | M | 2024-08-31 at 23:59:59 | |
| CP3a: fast solution with doubles | ||||||
Using all resources that you have in the CPU, solve the task as fast as possible. You are encouraged to exploit instruction-level parallelism, multithreading, and vector instructions whenever possible, and also to optimize the memory access pattern. Please do all arithmetic with double-precision floating point numbers. |
||||||
| – | – | 5 + 0 | ★★ | M | 2024-08-31 at 23:59:59 | |
| CP3b: fast solution with floats | ||||||
Using all resources that you have in the CPU, solve the task as fast as possible. You are encouraged to exploit instruction-level parallelism, multithreading, and vector instructions whenever possible, and also to optimize the memory access pattern. In this task, you are permitted to use single-precision floating point numbers. |
||||||
| – | – | 5 + 0 | ★★ | M | 2024-08-31 at 23:59:59 | |
| CP4: GPU baseline | ||||||
Implement a simple baseline solution for the GPU. Make sure it works correctly and that it is reasonably efficient. Make sure that all performance-critical parts are executed on the GPU; you can do some lightweight preprocessing and postprocessing also on the CPU. Remember to check all CUDA operations for errors. In this task, you are permitted to use single-precision floating point numbers. |
||||||
| – | – | 5 + 0 | ★ | M | 2024-08-31 at 23:59:59 | |
| CP5: fast GPU solution | ||||||
Using all resources that you have in the GPU, solve the task as fast as possible. In this task, you are permitted to use single-precision floating point numbers. |
||||||
| – | – | 10 + 0 | ★★ | M | 2024-08-31 at 23:59:59 | |
| CP9a: better algorithm | ||||||
Try to use Strassen's algorithm to speed up matrix multiplication. Reimplement your solution to CP3b so that it uses the basic idea of Strassen's algorithm. It is sufficient to use the basic idea of Strassen's algorithm (adapted to our task as needed) in the topmost levels of recursion; you can then fall back to the naive algorithm. A pure implementation of the naive algorithm, even if its is sufficiently fast, is not a valid solution for this exercise. Care is needed with rounding errors; you may need to resort to double-precision arithmetic to pass the tests. |
||||||
| – | – | 5 + 0 | ★★★ | M | 2024-08-31 at 23:59:59 | |
General instructions for this exercise
You are given m input vectors, each with n numbers. Your task is to calculate the correlation between every pair of input vectors.
Interface
You need to implement the following function:
void correlate(int ny, int nx, const float* data, float* result)
Here data is a pointer to the input matrix, with ny rows and nx columns. For all 0 <= y < ny and 0 <= x < nx, the element at row y and column x is stored in data[x + y*nx].
The function has to solve the following task: for all i and j with 0 <= j <= i < ny, calculate the correlation coefficient between row i of the input matrix and row j of the input matrix, and store the result in result[i + j*ny].
Note that the correlations are symmetric, so we will only compute the upper triangle of the result matrix. You can leave the lower triangle i < j undefined.
The arrays data and result are already allocated by whoever calls this function; you do not need to do any memory management related to these arrays. You should not assume that result contains any valid values at the point of call. In particular, it is not guaranteed to be initialized with zeros.
Details
The input and output are always given as single-precision floating point numbers (type float). However, depending on the task, we will do arithmetic with either single or double precision numbers:
- If the task specifies that you must use double-precision floating point numbers, then all arithmetic operations must be done with type
double, all intermediate results must be stored in variables of typedouble, and you will only round the final result to single precision. - If the task specifies that you can use single-precision floating point numbers, then you are encouraged to use the type
floatwhenever possible.
However, in each case you will have to make sure the numerical precision of the results is sufficiently high. The grading tool makes sure the error is sufficiently small. The error thresholds are chosen so that a straightforward and efficient solution is typically good enough, but please feel free to ask the course staff for hints if you are struggling with the rounding errors.
Examples
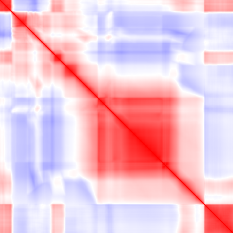
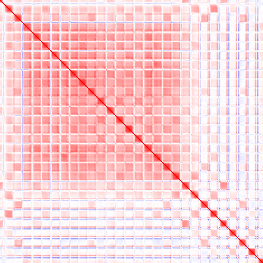
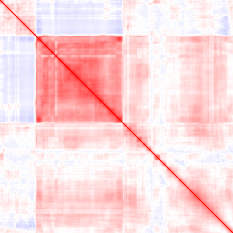
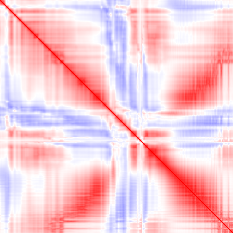
These examples show what a correct implementation will do if you apply it to a bitmap image:
- Input (first image): vector i = row i of the image.
- Output (second image): red pixel at (i, j) = positive correlation between rows i and j, blue pixel = negative correlation.
Hints
A reasonable way to calculate all pairwise correlations is the following:
- First normalize the input rows so that each row has the arithmetic mean of 0 — be careful to do the normalization so that you do not change pairwise correlations.
- Then normalize the input rows so that for each row the sum of the squares of the elements is 1 — again, be careful to do the normalization so that you do not change pairwise correlations.
- Let X be the normalized input matrix.
- Calculate the (upper triangle of the) matrix product Y = XXT.
Now matrix Y contains all pairwise correlations. The only computationally-intensive part is the computation of the matrix product; the normalizations can be done in linear time in the input size.